Phnet
PH-net:基于块硬度的半监督超声乳腺病变分割
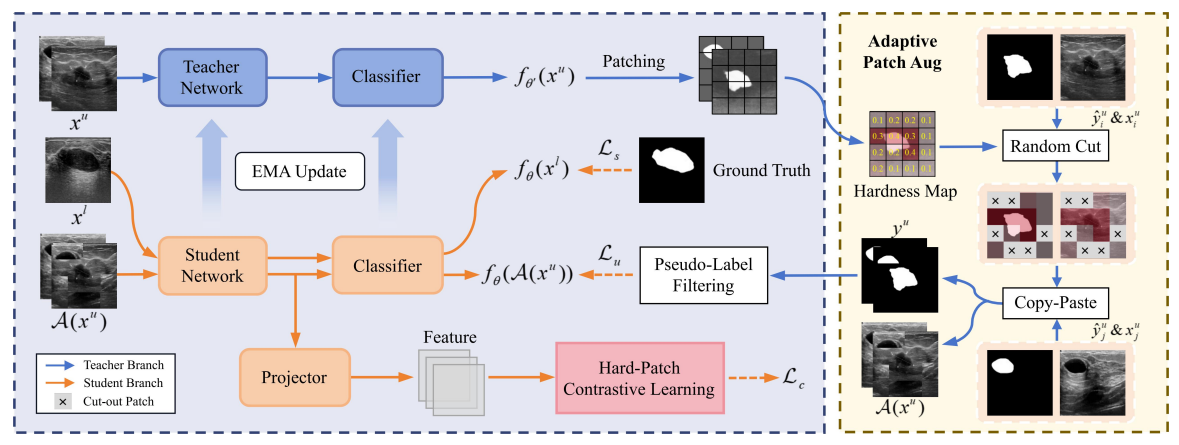
教师学生架构,教师网络用少量真实标签数据对进行训练,初始化教师和学生模型权重。对未标注数据进行分割(像素分类),然后进行分块,计算每个块的硬度,保留前K个最高硬度的块,对其他的块和对应块的伪标签进行替换(替换使用的是另一张未标注图像的对应块及其预测的伪标签)得到增强图像,学生模型对真实标签和增强图像对进行监督训练。同时用EMA对教师模型的参数进行优化,另外有分支进行块的对比学习,对硬块进行特征提取,对于每个锚点(anchor)特征向量,选择正样本(与锚点相同类别的特征向量)和负样本。对特征进行余弦相似度的计算,使同一类别的特征向量在特征空间中更接近,而不同类别的特征向量更远离。最后结合三个loss,分别是学生网络的有监督学习loss(真实图像标签对),无监督学习loss(增强图像伪标签对),和对比学习loss,优化总的loss得到最优模型权重。具体可以看下面细节
一些组件细节
块硬度:$r_m=-\frac1{\log C}\frac1{h\times w}\sum_{k=1}^{h\times w}\sum_{c=0}^{C-1}p_{m,k}(c)\log(p_{m,k}(c))$
块内的熵,值越高,不确定性越高,越难区分。$p_{m,k}(c)$是第$m$个块中第$k$个像素属于类别$c$的概率
EMA更新:
- 初始化:
- 在训练开始之前,教师网络的权重$\theta’$被初始化为学生网络权重的$\theta$初始值,即 。$\theta’=$ $\theta$
- 设置动量参数:
- 选择一个动量参数 $\alpha$,这个参数通常非常接近1(例如,0.999),用于控制新旧权重在EMA中的权重比例。
- 训练学生网络:
- 在每个训练步骤中,学生网络的权重$\theta$通过梯度下降法更新,以最小化损失函数。
- 更新教师网络权重:
- 在每个训练步骤之后,教师网络的权重 $\theta’$ 通过以下公式更新: $\theta’\leftarrow\alpha\cdot\theta’+(1-\alpha)\cdot\theta $
- 重复更新:
- 重复步骤3和4,直到训练完成。
Loss Function
$\mathcal{L}=\mathcal{L}_s+\lambda_u\mathcal{L}_u+\lambda_c\mathcal{L}_c$
一共由三部分loss组成
监督学习loss :标准的交叉熵损失
\[\mathcal{L}_s=\frac{1}{\lvert\mathcal{B}_l\rvert}\sum_{i=1}^{\vert\mathcal{B}_l\vert}\ell_{ce}(f_\theta(x_i^l),y_i^l)\]无监督学习loss:
\[\mathcal{L}_{u}=\frac{1}{\vert {\mathcal{B}_{u}} \vert}\sum_{i=1}^{\vert {\mathcal{B}_u} \vert}\sum_{j=1}^{H\times W}M_{ij}^{f}\cdot\ell_{ce}(f_{\theta}(\mathcal{A}(x_{ij}^{u})),y_{ij}^{u})\]-
$\vert \mathcal{B}_u \vert$ 是未标记数据批次的大小。
-
$H\times W$是图像的分辨率。
-
$M_{ij}^f$是一个掩码函数,\(M_{ij}^f=1\begin{bmatrix}\max(f_{\theta'}(\mathcal{A}(x_{ij}^u)))\geq\gamma\end{bmatrix}\)用于指示像素$(i,j)$是否应该被包括在损失计算中。
-
$\ell_{ce}$是交叉熵损失函数。
-
$f_\theta$是学生网络的前向传播函数。
-
$\mathcal{A}(x_{ij}^u)$是对未标记图像 $x_{ij}^u$应用的数据增强函数。
解释
- 数据增强:对未标记图像$x_{ij}^u$应用数据增强$\mathcal{A}$。
- 教师网络预测:教师网络对增强后的图像进行预测,生成伪标签。
- 置信度过滤:使用掩码函数$M_{ij}^f$来确定哪些像素的预测是可靠的。如果教师网络对某个像素的预测置信度超过阈值$\gamma$,则认为该像素的预测是可靠的。
- 损失计算:对于每个可靠的像素,计算学生网络的预测与教师网络生成的伪标签之间的交叉熵损失。
- 平均损失:将所有可靠像素的损失求和,然后除以未标记数据批次的大小,得到平均无监督损失。
对比学习loss:
\[\mathcal{L}_{c}=- \frac{1}{C\times\vert\mathcal{Z}_{c}\vert}\sum_{c=0}^{C-1}\sum_{z_{ci}\in\mathcal{Z}_{c}}\log\left[\frac{e^{(\langle z_{ci},z_{c}^{+}\rangle/\tau)}}{e^{(\langle z_{ci},z_{c}^{+}\rangle/\tau)}+\sum_{z^{-}\in\mathcal{Z}_{c}^{-}}e^{(\langle z_{ci},z^{-}\rangle/\tau)}}\right]\]-
$Z_c$是类别$c$的正样本特征集合。
-
$Z^{-c}$是类别$c$的负样本特征集合。
-
$z_{ci}$是锚点特征向量。
-
$z_c^+$是类别$c$的样本特征的中心 (可以是记忆库中存储的样本特征的平均值)。$\tau$是温度参数,用于调整相似度的分布。
- 锚点特征向量$z_{ci}$是从当前批次中选取的。
- 正样本$Z_c$和负样本$Z^{-c}$也是从当前批次中选取的,而不是从记忆库中选取。
- 对比损失函数$L_c$是基于锚点特征向量与正样本和负样本之间的余弦相似度来计算的。⟨·, ·⟩ 是两个特征之间的余弦相似度。
